Mammalian toxicity testing: in vivo, in vitro, multigeneration; C 2, 8, 9, 10, 20; Molecular methods, high throughput testing; C 9, 31

Mammalian Toxicology, Session 9

Mammalian toxicity testing: in vivo, in vitro, multigeneration; C 2, 8, 9, 10, 20; Molecular methods, high throughput testing; C 9, 31

The penultimate versions of projects should be submitted (via e-mail or the Web) over the next few days and all members of the class should review and comment on each of them over the next two weeks.

Analytical Considerations

Most of the topical coverage today turns on assays of various sorts. Forensic, clinical, and environmental toxicology all depend on the application of a battery of physical chemical methods along with a large array of biological test assays. There are common concepts that must be considered in running any and all of these analyses. Indeed, these questions arise whenever an analytical method is being developed and validated. Not just in toxicology, but in endocrinology, immunology, analytical chemistry, molecular biology, microbiology, etc. What is a real signal or response in a given assay? What is due to instrumental or biological background or noise? How reproducible are the signal versus input relationships? Do our predictions of the content of an analyte in a reference source agree with the known content, i.e., how accurate is the method used? Can the method sense the amounts of analyte present in a given test sample; how sensitive is the technique? Is the method specific for the analyte of interest, or does it respond both to the analyte and to other compounds that may be present in the sample which share some molecular feature but do not necessarily share biological impact?

Coverage of much of this material can be found in: Chan, Immunoassay: A Practical Guide, AP: Orlando, FL, 1987; Gosling, Immunoassays: A Practical Approach, OUP: Oxford, UK, 2000; Tietz, Textbook of Clinical Chemistry, Saunders: Philadelphia, PA, 1986; or Campbell & Wood, An Introduction to Quantitative Endocrinology, In Wood, Dynamics of Human Reproduction: Biology, Biometry, Demography, Aldine de Gruyter: New York, NY, 1994.

So, in running assays how do we account for alternative causes of signal and background signal? This requires being able to distinguish a signal due to the causative agent from a signal due to background noise. This is best accomplished by use of an assay that is well characterized and validated. For both bioassays and analytical assays this means the assay must operate within well-characterized ranges for a series of quality control parameters. These are criteria for valid assays:

1. Precision -- reproducibility (A given input results in a predictable output.)

2. Sensitivity (Limit of Detection) -- this is the lowest measurable, nonzero dose (e.g., LOAEL); also, in a chemical analytical sense, the slope of the response curve, dY/dX, the ability to differentiate one dose from the next.

3. Accuracy -- evaluation of reference standards yields expected results (as determined by an independent method or from a consensus of others running similar tests on the same standard materials)

4. Specificity -- the assay measures the intended analyte or parameter even in the presence of potentially interfering substances (lack of specificity = nonspecificity or cross-reactivity)

Bias is found when a result curve is obtained that is different from that seen in another assay. The idea combines sensitivity and specificity dimensions.

Note that a high signal to noise ration, S/N, implies a high analytical sensitivity. It will do well in discriminating the presence of signal from background.

All of these criteria can be expressed mathematically for any given assay. Precision is given as the coefficient of variation, CV, calculated as the standard deviation of replicate measurements of a single sample divided by the mean result for that measurement, SD/M. Intra-assay CV is computed from data within a single assay while inter-assay CV is computed across repeated assays of the same type. The inter-assay CV is analytically more important as it includes variance derived from all the minor day-to-day fluctuations that might impact the evaluation of a random unknown sample. Both CV computations are normally done on a reference standard or preparation that matches the makeup of unknown samples as closely as possible. Although this measurement can be done on as few as 2-3 replications, it is not normally considered valid until the number of replicates exceeds 20. This magic number, 20, is also the number of replicates normally used as the minimum for computing the other quality assurance parameters (accuracy, limit of detection) mentioned below. For a chemical analytical technique, an inter-assay CV less than 3-5% is common, while for bioassays an inter-assay CV of 15-30% may be acceptable. Obviously the lower the CV the more reproducible results will be and the better the estimates for analyte content in unknown samples will be. Some of this is reflected in the curves for assays and immunoassays that are reproduced below. Note how the precision error is propagated into the error of the estimate for unknowns.

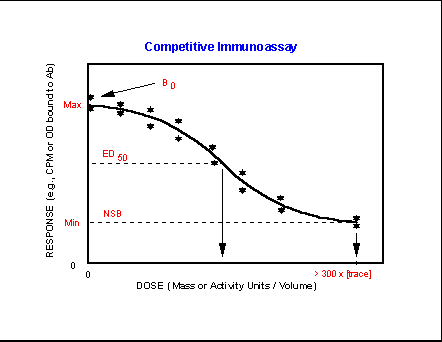
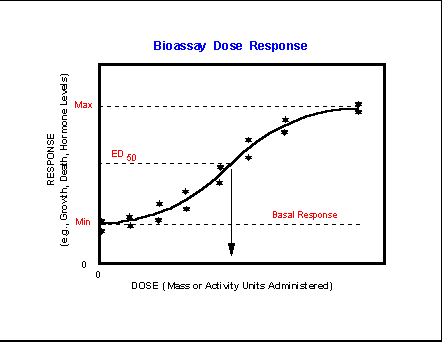
The basic shapes of response curves are shown along with the minimum, or nonspecific binding, NSB, or noise response obtained in the absence of any specific analyte or response of interest. Many assay responses are saturable and demonstrate an upper response or signal asymptote. In competitive assays this corresponds to the signal obtained in the absence of added analyte, B₀. The effective dose at 50% response, ED₅₀, corresponds to the K_m computed for enzyme assays.

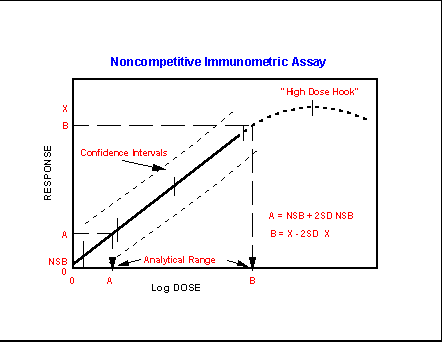
Noncompetitive binding assays resemble the curves obtained for many physical chemical analytical assays in that the signal rises nearly linearly for each increment of analyte added. The signal may or may not demonstrate an upper asymptote, or saturation, but often does. Note that in both competitive and noncompetitive situations there is a limited range over which the assay follows a monotonically changing (decreasing or increasing) tragectory. This is the useful analytical range. For any of the analytical curves there will be a degree of imprecision in measurement that will be greatest at the lowest and highest concentrations of analyte measured. In a strictly linear response assay this would be constant from one end of the assay response curve to the other. However, because noise makes up a substantial amount of the available signal or response at the lowest values and because it is rare for an assay technique not to become saturated at sufficiently high analyte loads, the deviation from linear error distribution is the rule rather than the exception. The “High Dose Hook” in a noncompetitive binding assay also often applies to instrumental methods where analyte loads above the point of saturation often decrease rather than increase the signal for any further increments of analyte.

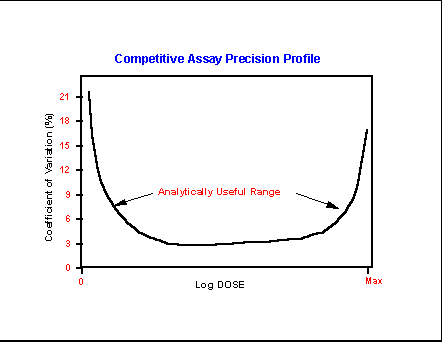Plotting CV versus analyte concentration produces a plot that demonstrates the expansion of analytical error that occurs at the lowest and highest analyte loads. Depending on the assay, the useful analytical range will spand the bottom, or near-linear portion of the “U” profile and include analyte levels within an acceptable error range. Outside that range error may negate the utility of the assay entirely. Or it may limit its use to a qualitative “yes” or “no” indication that the analyte levels are above or not above the levels seen as background noise.

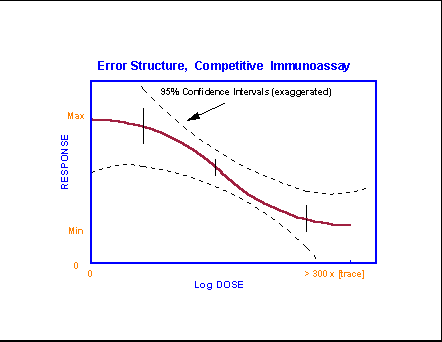
Looking at the Limit of detection for an assay usually means defining a level of analyte that, when added to a sample known not to contain the analyte beforehand, produces a signal that is statistically different from the signals found for repeated measurements of an uncontaminated sample, or zero control. This is normally defined as the analyte level (concentration or mass) that generates a response signal that exceeds the zero dose signal mean plus (or minus for a decreasing signal assay) 2 (or 3) standard deviations of the zero dose signal mean. This corresponds to the upper 95% (or 99%) confidence interval about the zero control signal mean. Note that precision contributes to this estimation as well as the actual sensitivity (slope of the analytical curve) of the measurement. Noise or background in an analytical system takes many forms: fluctuation of an electrical source leading to fluctuation in a photometric light source or the voltage across a photomultiplier tube, sunspot activity that can randomly alter the signal levels detected by a radiation counter, individual genetic variations among test animals that lead to differences in basal metabolic activities, chemical or temperature gradient differences among replicated cell or bacterial cultures arising from such variables as the position of the culture within the growth chamber, or fluctuations in vacuum systems arising from slight variations among samples in content of non-analyte volatile chemicals. Many of these cannot be readily controlled or they arise stochastically and are by definition uncontrollable.

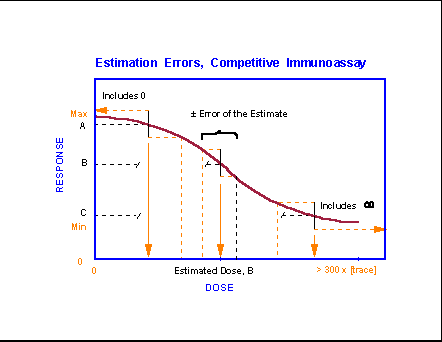While noise contributes primarily to limitations on the lowest level of analyte that may be reliably detected, other forms of imprecision (gravimetric errors, volumetric errors, timing errors) have equal impact on the estimation analyte levels above the zero value. Whenever an analytical method demonstrates a nonlinear response curve (almost always), there will be an area (shown for unknown A) in which the estimation error will cause a signal to be indistinguishable from a zero analyte level. And, there will be an area (shown for unknown C) in which the response will be indistinguishable from that found for an infinite (above saturation) level of the analyte. The useful analytical range, and the range in which reference standards should be prepared, falls between these two levels. Note how precision, reproducibility of estimation, particularly of known standards, controls the error of the estimate and the anticipated precision of the measurements.

Accuracy describes the ability of an assay to reproduce the value of a reference or control sample that has been either composed using direct gravimetric means or has been evaluated by an independent, previously validated, method. The National Bureau of Standards spends much of its time verifying methodologies and putting together reference preparations for all sorts of analytical techniques. The American Association of Clinical Chemists provides reference samples and a reference sample exchange program for clinical chemistry labs in which samples generated by the Association or key member laboratories are provided to participating laboratories and the collective results are compiled and compared to ascertain which laboratories and methods (if more than one is used) are accurately measuring the known content of the samples in question. Methods that measure single molecules or their fragments tend to be used as the reference methodologies to which all others are compared. They are the “Gold Standard” methods because of their absolute specificity, their sensitivity to the presence of any signal, and to their proportional response to increasing quantities of analyte. Their normal drawback is that they often require extensive manipulation of the sample prior to introduction into the analytical instrumentation. This is normally in the form of extraction or chromatographic separation of the analyte from the other components of the original sample matrix. Thus, these methods while exquisitely sensitive and specific, tend to be very time consuming and expensive with respect to sample preparation. For good reference materials this makes considerable sense. But for routine samples it is definitely an impediment and means that secondary methods are often the first used for routine diagnostics or analyses.

Sample matrix includes all those elements of a sample other than the analyte of interest. If there is nothing in the matrix that is capable of perturbing the analytical method being used, the entire sample, or a subsample of it, may be introduced directly into the assay. In that instance no change in the standard curve or its quality assurance parameters (precision, limit of detection, accuracy) should take place relative to what would be seen if pure analyte suspended in a neutral matrix like pure water, pure solvent, or cellulose paper were introduced into the analytical system. If, however, something in the matrix makes the analyte less accessible, e.g., adsorption to charcoal particles or serum binding proteins, or chemically resembles the analyte, e.g., shares key reactive groupings that are detected by a colorimetric reaction or is a metabolite of the analyte that can bind to antibodies raised against the analyte of interest, or is capable of inhibiting a reaction or response of interest, e.g., high acidity that will prevent an antibody binding reaction from occurring or the presence of compounds that inhibit Taq polymerase in a PCR assay, then the analytical protocol used must either extract the analyte from the sample matrix or neutralize the interference by otherwise manipulating the sample. If extraction is involved the recovery of analyte from samples with an identical or similar matrix must be determined so that corrections can be applied that recognize the losses that have occurred during this step of the analysis. Alternatively, a molecule with very similar characteristics can be added in known quantity to the sample prior to extraction, e.g., a tritiated or deuterated form of the analyte of interest, as an internal standard. Estimation of the content of internal standard after the extraction then allows for correction for this analytical step. In many molecular assays a probe or construct similar to that of analytical interest is included as a control. This often acts as an internal standard that can reflect procedural losses leading up to the final analytical measurement by techniques such as PCR, Southern blotting, or Northern blotting.

If extraction is not performed prior to introduction of the sample into an assay, several common manipulations may still allow differentiation of the analyte signal from those that might arise from any matrix components. Sample dilution often reverses adsorption of the sample onto particles or carrier proteins in addition to decreasing the concentrations of all components of the sample. If the analyte of interest has a steeper response curve than any competitors in the matrix, sufficient dilution may allow specific analyte detection even in the presence of matrix interferences. The problem here is to avoid dilutions that carry the analyte levels to those near or below the limit of detection of the method. Dilution of inhibitors may also obviate the need for extracting the analyte from the matrix prior to introduction into the assay. But simple sample manipulations may also accomplish the same thing: boiling may free an analyte from binding proteins or remove inhibitory enzyme activities or volatile components, acidification or alkalinization followed by neutralization may decompose analyte conjugates or interfering molecules, addition of an excess of enzyme substrate or a metal chelator may inactivate a competing enzyme, or selective precipitation of one or more classes of macromolecules may allow unfettered access to the analyte of interest. Finally, if there is ample reason to assume that virtually all samples to be examined will contain similar quantities of matrix interferences, the sample may be directly introduced into the assay so long as any standards or reference preparations are made up in a similarly comprised matrix.

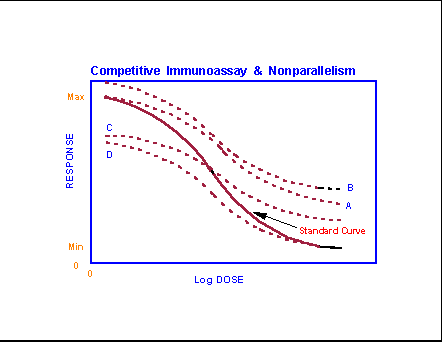The impact of several deviations from identical sample matrix composition can be seen in this figure which compares the results for a standard curve with those obtained by serially diluted samples. Plots A & B depict the loss of sensitivity that tends to occur in the presence of analyte binders which can either elevate the zero dose response by removing basal levels of analyte or flatten the response curve by decreasing the effective signal production by any increment in analyte. Plots C & D demonstrate the problems raised by the presence of cross-reactive molecular species which may suppress the signal for the zero dose (in competition assays, by competing with tracer for the binding agent) and then continue to suppress incremental analyte signal (C) throughout the analytical range, or suppress the signal only until sufficiently diluted (D). Note that combinations of such impacts often occur. All tend to change the shape of the response curves in any analytical method. The change in shape relative to the standard curve means that such assays demonstrate nonparallelism, i.e., the dilution curves are not superimposable on the curve for the reference standards. When this happens, unknown estimates cannot be reliably predicted on the basis of the parameters described for the reference standards or any control preparations that may be run routinely in the assay. In such circumstances, the assay will either have to be treated as a qualitative assay or a series of recovery standards must be prepared that covers the full analytical range. When these are assayed, they will define a line that can be used to provide correction factors appropriate to all dilutions used for the assay. Less ideal, they will describe a mean correction factor and error band that can be incorporated into any estimation errors for samples measured by this assay.

Specificity of an assay is reflected in this need to simplify the sample prior to analysis. If a method is absolutely specific, it will not display nonparallelism even if the sample is placed directly into the assay. Moreover, that assay will not respond to the presence of even closely related compounds. Cross-reactivity (%) as normally described, by the ratio of the amount of pure potentially cross-reactive compound needed to generate an assay response equivalent to the ED₅₀ for the analyte standard curve to the amount of pure analyte needed at the ED₅₀ x 100, is a semiquantitative estimate of how specific the assay method is. In some instances a lack of specificity is useful in allowing similar groups or families of molecules to be measured collectively. Often, however, specificity is required to make certain that accurate results are being obtained for the assay. Think about the possible end results if a diagnostic PCR assay happens to respond both to a targeted gene found in a pathogenic organism available only in cultures held within a Defense Department biological warfare facility and to a pseudogene present in a common commensal microbe.

Ultimately, most secondary methods of analysis need to be validated or compared to the results of Gold Standard methods. Or the analytical results of any type need to be compared with the clinical or pathological manifestations of toxicity, physiological response, or presence of disease. A pregnancy test needs to be verified against the number of clinical pregnancies actually seen in the weeks or months following testing. A test for measles needs to be verified against the actual manifestation of measles infection. Such comparisons among assays or against independent endpoints are often evaluated using a Chi-square approach where the distinct possible outcomes of the reference assay or evaluation (for example, development of disease or the known content of a compound) are placed on the X-axis and compared to the outcomes of the test assay (or drug trial) on the Y-axis. For a 2x2 evaluation where each test has yes or no answers (i.e., they are qualitative or semiquantitative) each of the cells can be readily described.

		Known Condition
		Positive	Negative
Test Result	Positive	True +	False +
Test Result	Negative	False -	True -

1. When both tests give positive assays, the result is entered in a square termed "true positives," TP.

2. When both are negative, the result is entered in a square termed "true negatives," TN.

3. When the reference test is positive, but the test assay is negative, the results are "false negatives," FN.

4. When the reference test is negative, but the test assay is positive, the results are "false positives," FP.

With this information, the test assay can be evaluated (relative to the reference) by five qualitative features (note that these are related but not identical to the same qualities defined by strictly analytical means): Sensitivity, Specificity, Predictive Value for Negative Responses, Predictive Value for Positive Responses, and overall Efficiency (or Accuracy).

1. Sensitivity = (TP/(TP + FN)); note, this is not the same as lowest measurable dose or slope of the curve for a single assay.

2. Specificity = (TN/(TN + FP)); this is related to, but not the same as measuring the intended parameter.

3. Predictive Value for a Positive Test = (TP/(TP + FP))

4. Predictive Value for a Negative Test = (TN/(TN + FN))

5. Efficiency = ((TP + TN)/(TP + TN + FP + FN)); this is the overall ability of the test to correctly predict or the presence of a compound or drug or of an assay having the expected result.

Because of these inter-related mathematical definitions, it should be evident that it is difficult to have assays that are entirely sensitive and specific at the same time. Indeed, it is often necessary to trade between these two qualities to generate an optimal assay that has the best efficiency (or accuracy) possible.

LOAEL, NOAEL, Zero Dose

Note how these appear differently in a sigmoid model of toxicity in which there is no difference between the beginning of the dose-response curve and zero dose, i.e., the response curve is monotonically increasing beginning at zero dose, and in the threshold model of toxicity in which there is an actual point on the dose axis above zero dose at which the response falls to zero.

In the monotonically increasing case, repeated measurements of the dose response curve provide an error estimate around the points of the dose curve including the zero dose. The mean of the zero dose + 2 (or 3) standard deviations of the zero dose, define a line through the dose response curve below which a response cannot be distinguished from the impact of a zero dose. Since doses are chosen for testing, any dose falling below the line just described would yield no effect. The highest dose below that line should be the NOAEL dose. The first dose above that line should be the LOAEL. Note the line defined could also be referred to as the maximal tolerated dose, MTD.

The threshold model is a variant of the linear extrapolation model. The latter assumes there is no dose that does not have some effect. If our methods are sensitive enough, this model would, in fact, have no NOAEL or MTD. If, more realistically, there are physiological mechanisms that pose barriers for toxicity, e.g., detoxification systems, sequestration mechanisms, or repair processes, there will be a dose that does not generate a response in the organism. In this situation, there will be no response at a finite, nonzero, dose which can be termed the NOAEL or the MTD. The first dose above that level would be the LOAEL. Operationally, it is normally impossible to distinguish between a true threshold model and a sigmoid model given the limits of response measurement technologies and the finite number of dosages that can be tested. Thus, the determination of NOAEL, LOAEL, and MTD fall back to the approach outlined above under the sigmoid model.

What happens with delayed effects? Cancer, neurodegeneration, immunocompromise (where opportunistic infections by secondary agents may actually be the ultimate causes of the observed toxic effect). In all these situations the phase delay between exposure and toxic response may be difficult or impossible to detect above background "noise." But the obvious places to begin exploring these situations are in the tissues most potentially affected. In the case of cancer this would probably be most prominent in the tissues demonstrating the most active proliferation: testicular germinal epithelium, bone marrow, lining of the small intestine, placenta, or embryonic tissues. Note how the clearance and repair processes make the connection of cause and effect even harder because the causal agent may be cleared long before the impacts of its effects are expressed by the biological systems triggered to set in motion processes or cascades that are proximally responsible for observed effects.

Practically, these delays have important impacts on the process of testing drugs and food additives since they may take 10-20 years or more to become apparent. Current patents are only good for 17-20 years including much of the time needed for the later phases of testing. There is little wonder companies try to optimize profits through the course of the initial patent as they need to address the costs not only of development, but also of liability litigation that may arise as a result of delayed untoward effects that may not be made apparent during the time of testing. Animal models are not perfect substitutes for humans and not all humans can be adequately modeled even with other humans.

So the question arises as to whether the potential for delayed deleterious toxic effects might be grounds for delaying the granting of a patent, prolongation of the testing phase, governmentalization of the responsibility for prolonged testing, or automatic patent renewal if no such deleterious effects are reported during the initial patent.

Available Assays

While C&D provides a lengthy list of methodologies for biological assays involving mutagenesis and carcinogenesis their coverage of analytical methods is quite weak. I would refer you to any good current analytical chemistry text for information on instrumental methods such as: colorimetry, spectrophotometry, fluorimetry, radiometry, flow cytometry, quantitative cytology and image analysis, detection methods for gas and liquid chromatography (electron capture, radiometry, ionization, flame photometry, refractive index, and spectrophotometry), thin layer chromatography, nuclear magnetic resonance spectrometry, mass spectrometry, PCR, quantitative electrophoresis, dot-blotting, electron microprobe analysis, flame photometry, atomic absorption spectrometry, and microarray analysis. A search on Google for any of these terms will often turn up libraries and professional association pages containing specifics and peculiarities of each of these methods. Not all of them require sample extraction prior to application and many are becoming more widely adapted for use in high throughput laboratories.

Particular cases in point for high volume analysis are various versions of spectrophotometry, automated chromatography (gas, liquid, thin layer), and microarray analyses. By using robots to subsample, extract, concentrate (via lyophilization or solid-phase extraction followed by elution into more favorable solvents), and apply or inject samples into microplate wells or onto chromatography columns, many labor intensive methods have moved from the research laboratory to the clinical, pharmaceutical, or toxicological laboratory where huge numbers of samples are processed in a given year.

Automation allows immunoassays in a variety of formats, cell and microbial cultures, and even protein or nucleic acid mass spectral analyses to be performed nearly unattended between sample loading and endpoint readout. In all these cases the validation and development work on the methods provides the substrate for confidence in the overall results when it is coupled with use by operators that monitor the appropriate quality assurance parameters and that interpret the results with full understanding of the actually unattended operations taking place.

The use of microarrays are particularly important in toxicological analyses because these are now being prepared to allow demonstration of DNA matching most of the genetic loci in several different organisms, RNA matching those expressed in cells of several different tissues in each of several species, and proteins expressed in several different tissues in each of several species. Thus, tools are now being constructed that will allow investigators to look at tissue samples from intoxicated subjects and determine if these tissues contain damaged DNA, and altered patterns of RNA or protein transcripts relative to those of unintoxicated individuals. The primary need in this area currently are improvements in methods for collecting, collating, and associating the information gleaned from each of the thousands of data points collected on each individual chip while at the same time maintaining good quality assurance values for precision, accuracy, specificity, and sensitivity for each element in the array being used.

Note also the differing goals of toxicological forensic laboratories and clinical toxicological laboratories as noted in C&D. The former is often attempting to push assay sensitivity limits to deal with small samples or low toxicant loads and is frequently forced to use qualitative results (detectible vs nondetectible) while the latter is frequently most concerned with quantitative results that allow medications to be held to the effective but nontoxic range.

While an exhaustive list of methods and related sites is beyond the scope of this course these are appropriate for looking up toxicological methods and applications.

ASTM testing methods:

chronic oral toxicity: http://www.astm.org/DATABASE.CART/PAGES/E1619.htm

ASTM Bioassay Table:

http://www.dtsc.ca.gov/ScienceTechnology/bioassay/Table.html

Discussion Questions

NOAEL, LOAEL & Threshold Model (QS2Q2)

12. Are the concepts of NOAEL and LOAEL most compatible with a threshold level or a no threshold level conception of dose responses? How are they represented on dose-response curves? How do they differ from zero dose? Does the last answer change for environmental exposures if newer methods allow lower limits of detection for the toxicant in question?

Toxicology Information (QS2Q5)

15. Search out the following sites and explore them: HazDat, EXTOXNET, RTECS, Toxline, IRIS, IARC. What information do they contain? Do they appear up to date? Print out some examples of the contents and see if you can interpret them. To what area(s) of toxicology are each of them relevant?